Gra w życie: czterdziestopięcioletni symulator ewolucji

Gra w życie (The game of life) obchodzi w tym roku czterdzieści pięć lat. Zrodzona w umyśle Johna Hortona Conway'a, a spopularyzowana przez znanego wielbicielom matematycznych łamigłówek Martina Gardnera do dziś jest eksploatowana i inspiruje wielu naukowców, głównie matematyków i teoretyków ewolucji. Czym jest ten bardzo prosty w założeniach program i co w nim takiego wyjątkowego?

Conway, urodzony w 1937 roku, jest jednym z najbardziej znanych matematyków. Od najmłodszych lat wykazywał duże zainteresowanie tą dziedziną i już w wieku 11 lat postanowił, że w przyszłości zajmie się nią zawodowo. Zainteresował sie teoriami z lat czterdziestych XX wieku, kiedy to John von Neumann pracował, zresztą z powodzeniem, nad stworzeniem teoretycznej maszyny, która według skomplikowanych reguł kopiowała wprowadzoną informację. Conway po latach badań znacząco uprościł system. W 1970 roku Grę w życie, bo tak został nazwany eksperyment Conway'a przedstawił na łamach American Scientist Martin Gardner, uwielbiany przez czytelników, wieloletni twórca rubryki dotyczącej matematyki Gry matematyczne w wyżej wymienionym piśmie. Gra w życie z rzutu zyskała olbrzmi poklask, uznanie i popularność, wręcz kult. O co tu w ogóle chodzi?

Reguły są zaskakująco proste. Gra w życie jest tak zwaną „zero player game”, czyli po wprowadzeniu danych wejściowych pozostawiamy ją samą sobie nie ingerując w jej przebieg.  Rozgrywa się w przestrzeni dwuwymiarowej, mamy więc nieskończoną siatkę komórek, które reprezentowane są przez kwadraty (choć nie zawsze, ale skupmy się na regułach Conway'a). Każda komórka ma ósemkę sąsiadów, czyli komórek bezpośrednio przylegających do niej ścianami lub rogami. Komórki mogą istnieć tylko w dwóch stanach: są albo martwe, albo żywe. Stany zmieniają się w równych odstępach czasu, cyfrowo moglibyśmy nazwać je „klatkami”, nazwijmy je jednak generacjami. Wszystkie komórki po zbadaniu stanu i położenia siebie i sąsiadów zmieniają się jednocześnie w zależności od tego stanu dając początek kolejnej generacji, czyli ewoluują. I tak w kółko. Istnieją tylko dwie reguły, które określają działanie gry:

• martwa komórka, która ma dokładnie trzech sąsiadów (czyli trzy sąsiadujące komórki są żywe), staje się żywa w kolejnej generacji ,
• żywa komórka z dwoma lub trzema żywymi sąsiadami nadal pozostaje żywa, w każdym innym stanie umiera w następnej generacji (z samotności lub zatłoczenia).

To wszystko. Banalnie proste, jednak niesamowicie zaskakujące. Naszą ingerencją jest jedynie wprowadzenie danych wejściowych, czyli ustalenie rozmieszczenia żywych komórek na „martwej” przestrzeni. Po ich wprowadzeniu obserwujemy zachowanie komórek i ich ewolucje. To co się dzieje na ekranie (ustalmy, że grę w życie odpalamy na komputerze, choć początkowo robiono to na papierze) może wprawić w osłupienie. Te reguły definiują Grę w życie jako automat komórkowy (czyli w skrócie: rozmieszczenie komórek i obserwacja ich ewolucji zgodnie z ustalonymi z góry zasadami).
Prawdą jest jednak, że aby zaobserwować NAPRAWDĘ ciekawe rzeczy w Grze w życie trzeba poznać mechanizm działania reguł i przyswoić sobie kilka prawd. Całkowicie losowe rozmieszczenie kilku lub kilkunastu (a nawet kilkudziesięciu, kilkuset) komórek zwykle prowadzi szybko do zakończenia ewolucji, pozostawienia trwałych artefaktow i statków (o których napiszę niżej). Co ciekawe nawet najmniejsza zmiana, na przykład wprowadzenie w pierwotną strukturę jednej komórki może diametralnie zmienić ewolucję. Poniższy obrazek pokazuje cztery stany początkowe będące wariacjami na temat jednej losowo wprowadzonej struktury. Pierwsza z nich w generacji 19 zniknęła całkowicie. Druga struktura, gdzie usunąłem jedną komórkę, w trzeciej generacji zmieniła się w oscylator działający w nieskończoność. W trzeciej do pierwotnej struktury dodałem tylko jedną komórkę i system zmienił się w podróżujący po powierzchni (w nieskończoność) statek, o którym napiszę niżej. W czwartym stanie  z kolei dodałem komórkę w innym miejscu, system rozwinął się, by w 1107 generacji utworzyć kilka artefaktów i prostych oscylatorów. Jak widać pozornie małe zmiany w dużym stopniu wpływają na efekt końcowy.

No dobrze, mamy więc migający od mijających generacji ekran i chaotycznie poruszające się komórki. Skoro Gra w życie ma reguły, to musi być tu jakiś porządek. Owszem jest, dlatego też wyjaśnię pojęcia, które pojawiły się wyżej, oscylator i statek.

Jest kilka struktur, które tworzone są za pomocą określonego wzoru i można je często dostrzec na ekranie.

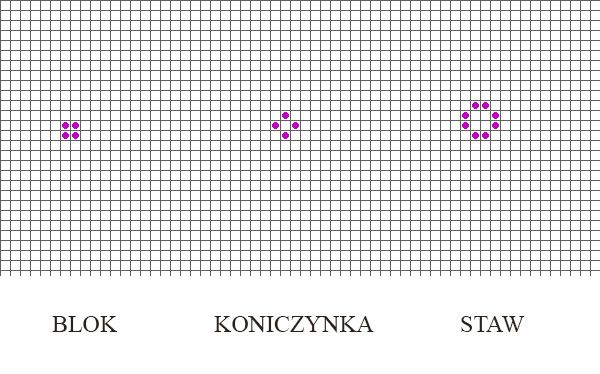
Najczęstszymi są tak zwane struktury stałe, statyczne czyli niezmienne w czasie układy, które często są końcowymi etapami ewolucji układu. Najprostszą z nich jest blok, czyli kwadrat 2 na 2. Inne to na przykład staw, bochenek lub koniczynka. Przyjrzyjmy się najprostszemu z nich, blokowi, i postarajmy się zrozumieć reguły automatu Conway'a. Blok utworzony jest z czterech komórek ułożonych w kwadrat. W związku z tym każda ŻYWA komórka ma trzech sąsiadów, dzięki czemu pozostają one żywe. Komórki martwe, które otaczają blok mają dwóch lub jednego sąsiada, w takim razie, zgodnie z pierwszą zasadą nie mogą stać się żywe. Blok nie zmieni się w czasie.

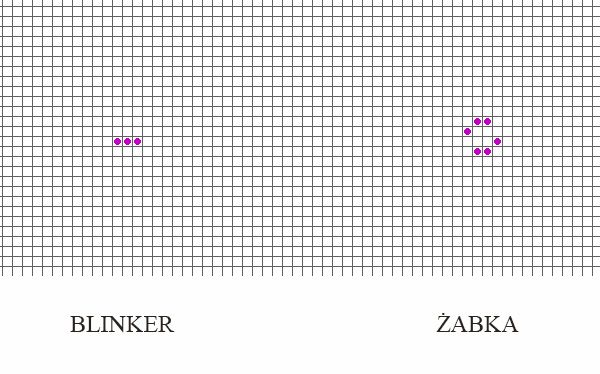
Drugim typem są oscylatory, czyli struktury, które zmieniają się w czasie (okresowo), ale w końcu powracają do pierwotnego stanu i powtarzają cykl. Są nieśmiertelne, czyli trwają w nieskończoność. Prostym przykładem jest blinker, czyli trzy żywe komórki ustawione w rzędzie (to on powstał w przykładzie czterech struktur  przedstawionym wyżej). Cykl trwa dwie generacje (okres równy 2), podczas których blinker ustawia się raz pionowo, raz poziomo. Weźmy go jako przykład do zrozumienia działania automatu. Blinker tworzą trzy komórki ustawione (powiedzmy) pionowo. Środkowa komórka ma dwóch żywych sąsiadów, więc w następnej generacji pozostanie żywa. Dwie pozostałe komórki mają tylko jednego żywego sąsiada, więc stają się martwe w następnej generacji. Z kolei prawie wszystkie martwe komórki nie spełniają pierwszej zasady, więc pozostaną martwe. Prawie wszystkie, bo komórki po lewej i prawej stronie środkowej żywej komórki mają dokładnie trzech żywych sąsiadów, więc w następnej generacji ożyją. Wynikiem tego w drugiej generacji powstanie system złożony z trzech poziomo ustawionych komórek. Po sprawdzeniu stanów wszystkich komórek układ w trzeciej generacji powróci do pierwotnego stanu. I tak w nieskończoność. Trochę zawiłe, ale powinno tłumaczyć działanie conwayowskiego systemu.

Inne proste oscylatory mają okresy równe 3,4, 8, a niektóre z nich powtarzają cykl po kilku tysiącach (!) generacji, z kolei oscylator o nazwie biały rekin ma okres 150000034! Tak, cykl powtarza się po tylu generacjach.

To były najnudniejsze struktury. Następne są znacznie bardziej ciekawe.

Statki to struktury w nieskończoność podróżujące po siatce kwadratów. Przez wiele lat zastanawiano się, czy w ogóle istnieje taka wędrująca struktura, ba, wyznaczono nawet nagrodę dla tego, kto ją znajdzie. Rozwiązanie okazało się bardzo proste. Szybowiec (glider), bo tak nazwano ten statek, składa się pierwotnie tylko z pięciu żywych komórek, ma okres 4, przy czym cykl kończy się w o komórkę innym miejscu niż poprzedni (po skosie). Szybowiec dzięki temu przemierza płaszczyznę w nieskończoność. Jest to jedna z najważniejszych struktur w całym automacie, ponieważ z racji swojej prostoty i łatwości powstawania "w locie" jest przekaźnikiem komórek pomiędzy powstającymi odrębnie strukturami. Glider okazał się tak ważny i popularny w świecie informatyków, że ustanowiono go jako symbol hakerów.

Prócz glidera jest jeszcze kilka innych statków. Pewnym rozwinięciem są tak zwane statki kosmiczne, bardziej skomplikowane struktury mogące przemieszczać się w inny sposób, o większym okresie, a także pewnych możliwościach modyfikacji. Potężne, kilkuset komórkowe statki tworzone przez pasjonatów (przyznajmy to, głównie informatyków) przyjmują wyszukane formy.
Jeszcze ciekawsza jest grupa struktur zwana działami (guns). Są to układy komórek, które podczas swojego cyklu wypuszczają statki. Ponieważ działo prócz tego, że ma być swojego rodzaju oscylatorem musi jeszcze generować układy (statki) żyjące własnym życiem. Są to skomplikowane struktury mające okres trwający nawet kilka tysięcy generacji, utworzenie ich jest bardzo trudne. Co ciekawe najmniejsze działo zadziwia wręcz swoją prostotą: to złożony z kilkudziesięciu komórek Gosper Glider Gun, który ma okres równy jedynie 30 i w tym czasie wypuszcza glidery z zaskakującą częstotliwością.
Do tego dochodzi cała masa innych ciekawych struktur: super statki kosmiczne, które przesuwając się po płaszczyźnie zostawiają za sobą nieruchome artefakty, puffery (najbardziej skomplikowane struktury, te z kolei dzielą się na inne) ogrody edenu, czyli struktury, które nigdy nie powstaną wskutek ewolucji. Jest tego bardzo dużo i wciąż są one rozwijane, wciąż odkrywane nowe. Program, którego sam używam i polecę na końcu artykułu dostarczany jest za darmo z całą masą bardzo ciekawych struktur. Ponieważ gameplay.pl nie daje możliwości  wstawiania gifów, a struktury polegają na ruchu, ciężko jest na podstawie obrazków w pełni docenić ich wspaniałość. Przedstawię tylko kilka z nich:

Działo oparte na czterech spiralach będących rogami kwadratu, a pomiędzy nimi nieruchome artefakty. W środku pulsujące jądro. Skomplikowana struktura wędruje od spirali do spirali. Co około 800 generacji wypuszcza w przestrzeń jeden szybowiec (nazwa pliku: spiral)

Potężna struktura o populacji 983 w pierwszej generacji składa się z kilku różnych, mniejszych zorganizowanych struktur. Jest to swojego rodzaju działo należące do grupy sawtooth wypuszczające podwójne statki, które zaznaczyłem na niebiesko. Obserwując jego rozwój można dojść do wniosku, że trwa w nieskończoność, ale autor zaznacza, że populacja z czasem się zmniejsza. Ciekawostką jest fakt, że co jakiś czas następuje swoisty zwrot i wypuszczone statki "kasują się". Zjawisko następuje w okolicach 1800, a potem około 60.000 generacji (nazwa pliku: sawtoot3)

Układ stworzony z dwóch struktur - jedna jest lustrzanym odbiciem drugiej. Struktury odsuwają się od siebie (dolna w lewy dolny róg, górna w prawy górny róg) przerzucając między sobą szybowce zaznaczone na niebiesko. Przedstawiony został stan z 185 generacji (nazwa pliku: loop)

Magiczna struktura. Obrazek przedstawia generację 1 złożoną z 615 komórek (123 szybowce). Szybowce poruszają się do wewnątrz, by w 656 generacji stać się oscylatorem o okresie 3 i liczbą komórek wahającą się między 44 a 48. Zaznaczyłem go niebieską pętlą, nie jest oczywiście częścią pierwotnego "X" złożonego z szybowców (nazwa pliku: makehslr)

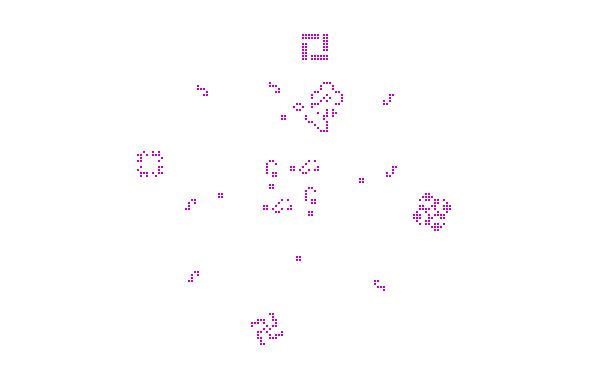
Struktur i zespołów struktur powstało wiele. Te najbardziej skomplikowane potrafią podawać liczby pierwsze i rozwiązywać proste równania, a nawet pisać teksty! Dowodami na to, że Gra w Życie wciąż jest żywa i kryje wiele niespodzianek są wynalazki z ostatnich lat: w 2010 roku stworzono strukturę zwaną Gemini, która porusza się na ukos, kopiuje się i niszczy strukturę macierzystą. Z kolei w 2013 roku utworzono pierwszego w historii replikatora, który nie dość, że klonuje siebie, to jeszcze przekazuje w o wiele mniejszym pakiecie komórek instrukcję tego klonowania.

A to tylko reguła Conway'a. Widzicie, w automacie komórkowym w stylu Gra w życie można ustanowić własne reguły, jest nawet specjalny zapis pozwalający na przekazywanie sformułowania. Reguła Conway'a zapisywana jest jako 23/3. Przed ukośnikiem zapisuje się ilość komórek w sąsiedztwie, dla których komórka przeżywa, dla Conway'a jest to 2 i 3. Za ukośnikiem wpisujemy liczbę komórek w sąsiedztwie, dla których komórka staje się żywa, tutaj jest to 3. Możliwość modyfikacji tych liczb pozwoliła na stworzenie wielu ciekawych reguł. Nie będę się o nich rozpisywać, ponieważ ta Conway'a jest najpopularniejsza i najprostsza. Są strony (podam je na końcu), które w przejrzysty sposób je katalogują. Wśród nich są takie smaczki jak reguła, według której struktury z czasem tworzą miasta otoczone murem, gdzie centralne części są w chaotyczny sposób aktywne, a otoczone są nieruchomą barierą  (2345/45678), reguła w malowniczy i niepokojąco organiczny sposób tworząca labirynty (12345/3), albo taka, której to granice są bardzo aktywne, a środki zbite i stabilne (5678/35678).

Oczywiście modyfikacje nie skończyły się na zmianie dwóch podstawowych reguł. Powstały automaty komórkowe, gdzie komórki nie są kwadratami, a trójkątami lub sześciobokami foremnymi. Są reguły, które przewidują istnienie trzech lub nawet więcej stanów komórki, albo ograniczające jej żywotność (na przykład komórka nie może być żywa dłużej niż 200 generacji). Wprowadzono także trzeci wymiar znacznie komplikując działanie automatów. Przedstawianie poszczególnych pomysłów mija się z celem tego artykułu, bo stałby się nieprzyjemnie długi, a tłumaczenie zasad ich działania może mnie przerosnąć, ponieważ nigdy nie sięgałem w automaty poza regułę Conway'a i jej bezpośrednie modyfikacje.

Labirynty utworzone z kilkukomórkowej struktury. Generacja 938, populacja liczy ponad 130.000 komórek. Reguła 12345/3

Dochodzimy w tej chwili do pewnego zwieńczenia tego tekstu, w tym miejscu powinniśmy sobie zadać pytanie: Po co to wszystko? Zanim przedstawię czemu Gra w życie tak pociąga szereg naukowców różnych dziedzin warto zwrócić uwagę na najbardziej podstawową wartość edukacyjną programu. W dość przejrzysty sposób tłumaczy działanie systemu zero jedynkowego. Wszak komórka może posiadać dwa stany: żywa (1) i martwa (0), a narzucone reguły sprawiają, że system działa według ich zasad. Co prawda uważam, że jest prostszy i znacznie bardziej obrazowy sposób na wytłumaczenie tego systemu (uwaga, Minecraft), ale Gra w życie też swoje przedstawia. Najprostszym komputerem bazującym na systemie zero jedynkowym jest eksperyment myślowy nazwany Maszyną Turninga. W skrócie: korzystając z tego systemu i pewnych reguł możliwe jest wykonanie wszystkich działań algebraicznych pod warunkiem, że dysponujemy nieskończoną ilością taśm i nieskończoną ilością czasu na cięcie i sklejanie. I wiecie co? Maszynę Turninga udało się odtworzyć w Grze w życie na regułach 23/3.  Prowadzi nas to do jednej myśli: Gra w życie może rozwiązywać wszystkie działania matematyczne. Jeśli tak, to czy może symulować bardziej złożone rzeczy?

Owszem. Okazuje się, że Gra w życie i inne automaty komórkowe prócz pewnych walorów rekreacyjnych stała się podstawą do badań prowadzonych przez całą rzeszę naukowców. Matematycy i informatycy to tylko część. Reszta to biolodzy, chemicy, biochemicy, fizycy, technolodzy czy nawet graficy i kompozytorzy. Symulacje prowadzone przez różnego rodzaju automaty o rozmaitych regułach wykorzystywane są przy rozwiązywaniu równań różniczkowych, badaniu zachowań ciał sypkich i gazów, symulowaniu rozprzestrzeniania się pożarów i epidemii, korków ulicznych, zachowań stadnych, rozwoju i ewolucji organizmów, rozwoju infekcji, pomagają nawet w tworzeniu generycznych tekstur, a także tworzeniu sekwencji muzycznych. Wszystkie te badania napędzane są przez paradygmat systemowy, którego pojęcie ewoluowało w czasie, ale najprościej mówiąc chodzi o rozbicie całości problemu na mniejsze części składowe w poszukiwaniu reguł rządzących tym problemem. Okazuje się, że im bardziej wgłąb tym znajdujemy coraz prostsze reguły. To właśnie pokazuje nam Gra w życie: dziecinnie proste reguły potrafią w określonych warunkach tworzyć i symulować złożone zachowania całych kolonii. Celem jest odtworzenie skomplikowanych zachowań za pomocą jak najprostszego programu. Załóżmy, że istnieje automat komórkowy opierający się na czterech stanach komórek, dwóch, trzech regułach dotyczących ożywania i umieralności i ten automat symuluje zachowania stadne. Celem i podstawą zrozumienia będzie przełożenie tych samych zachowań do prostszego automatu, co pozwoli rozłożyć problem na jeszcze prostsze reguły, a to da możliwość zrozumienia najbardziej fundamentalnych reguł rządzących zachowaniami stadnymi.

Stożek tekstylny (Conus textile) to jeden z najbardziej jadowitych ślimaków świata. Wzór na jego muszli do złudzenia przypomina wynik działania jednowymiarowego automatu komórkowego Wolframa o regule 30. Czy komórki muszli są automatami wykonującymi algorytm do utworzenia wzoru? (zdj. wikipedia)

Czy można na przykład stworzyć Grę w życie w Grze w życie? Można, nawet wykonano pewną strukturę złożoną z bodaj siedmiu milionów komórek, które symulowały prosty oscylator. Jeśli możemy stworzyć coś takiego, to gdzie znajduje się granica? Jeśli stworzyliśmy prosty oscylator z milionów komórek, stworzyliśmy struktury rozwiązujące zadania, piszące teksty, samoreplikujące się, ba, klonujące, to czy da się stworzyć coś bardziej skomplikowanego na bazie reguł Conway'a? Na pewno. W tej chwili zaczynają się rodzić bardzo dziwne pytania: czy da się symulować zachowania ludzkie? Inteligencję? Całe społeczeństwa, planety? Wszechświat? W jakim momencie jesteśmy jeśli chodzi o symulowanie komórkowe? C

em rządzi pewien prosty algorytm? Co jeśli jesteśmy tylko programem, tylko bardzo, bardzo skomplikowaną strukturą w olbrzymim komputerze na którym ktoś odpalił Grę w życie?

Jeśli jesteś zainteresowany Grą w życie polecam skorzystanie z poniższych linków:

Program, którego ja używam. Prosty, przejrzysty i nieskomplikowany w użyciu. Można zmieniać w nim reguły, wraz z plikiem dostajemy dodatkowo mnóstwo struktur do obejrzenia wraz z krótkim opisem.

Polska wikipedia. Zawiera usystematyzowany spis najbardziej podstawowych struktur, a także listę modyfikacji Gry w życie.

LifeWiki. Strona wiki poświęcona Grze w życie.

Na koniec filmik będący ukoronowaniem tego co pisałem o strukturach w Grze w życie. Pokazuje nie tylko proste struktury, jak najprostsze działo, ale też potężne i skomplikowane twory, które zaskakują i robią duże wrażenie tym w jaki sposób działają dzięki tak prostym zasadom.